The Introduction page contains several examples of how DAEPACK can be used, including: standalone mode, where the individual DAEPACK components are assembled with the users model and other numerical routines to solve a wide variety of problems, within an equation-oriented process simulator (e.g. ABACUSS II) to properly incorporate FORTRAN models (e.g., physical property routines and legacy models), and as an enabling technology for the construction of CAPE-OPEN components. Recently, we've proposed another application for DAEPACK: as an enabling technology for novel graphical/symbolic environments for numerical problem solving. A proposal has been sent to the MIT/Microsoft Project I-Campus and can be viewed by following this link.
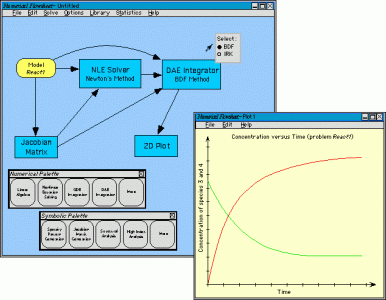
We envision a high-level graphical interface to the symbolic and numeric components of DAEPACK. Within this environment, the DAEPACK components would be represented as icons. The user would code a FORTRAN model of a system of equations and this model too would be represented as an icon. A "numerical flowsheet" can then be constructed by dragging and dropping the numerical and symbolic components onto the screen along with the users original model. The input and output relationships between these components can be established by drawing a set of arrows between the icons. If additional symbolic information (e.g., a Jacobian evaluator) is required or desirable for a calculation, an instance of a symbolic component can be created and applied to the user code by connecting it in the appropriate fashion. The resulting graph represents the overall calculation process required to solve a problem with a particular algorithmic strategy. For example, the solution of a hybrid discrete/continuous dynamic simulation from steady-state initial conditions will require the creation of a macroscopic algorithmic strategy that co-ordinates nonlinear equation solvers (to compute the steady-state and reinitialization at events), ODE or DAE integrators, and event location algorithms that may also rely on one dimensional root finding components. More advanced users and instructors, or students as part of their educational experience, may wish to code their own numerical components and integrate them into these macroscopic algorithmic strategies.
The figure below illustrates what this system may look like.