The symbolic components described above are exploited in a suite of DAEPACK numeric components. All of these components are also available as standard FORTRAN subroutines which can be incorporated into a program just as one would use LINPACK or ODEPACK routines. Three of these components are described below.
Block Solver
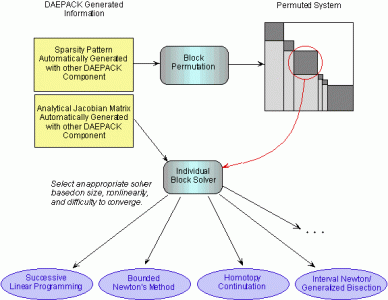
The automatically generated sparsity pattern and Jacobian matrix are used by the block solver component of the DAEPACK numerics library. This component uses the sparsity pattern of the system of equations and determines row and column permutations that convert the incidence matrix into block lower triagonal form. With this information, a solution to the overall system of equations is obtained by solving sequentially the diagonal blocks, smaller subsets of equations and variables. Based on the size and nonlinearity (this information can also be extracted automatically from the model equations), an appropriate solver is used. For example, if the subset of equations corresponding to a block are polynomial then appropriate solver can be used to reliably obtain all solutions. The figure below describes this sequential solution process.
DSL48SS
DSL48S is a component for DAE integration and parametric sensitivity
calculation. DSL48S features:
- Evolved from DASSL, a very robust and well-tested DAE integrator.
- Sparse linear algebra using Harwell Library's MA48 routines.
- Dynamic bounds checking.
- Automatic scaling of the corrector matrix.
- Modification for solution of high index systems using the method of dummy derivatives.
- Option for efficient parametric sensitivity calculation, Feehery et al. (1997)[11].
DSL48S uses the sparsity pattern and Jacobian matrix automatically generated by the other DAEPACK components.
DSL48E
DSL48E is component for performing hybrid discrete/continuous dynamic simulation and parametric senstivity calculation of DAEs. DSL48E calls DSL48S to take an integration step then searches the integration step using the state event location alorithm developed by Park and Barton (1996)[13]. This algorithm computes reliably the state events and guarantees the proper state event is found (i.e., the earliest event over the integration step) while avoiding the phenomenon known as discontinuity sticking. To use DSL48E (as well as other advanced state event location algorithms), the user would ordinarily have to provide explicitly the discontinuity functions contained within the model as well as be able to lock a discontinuous model into a particular discrete mode. However, with the discontinuity locking componenet of DAEPACK, this is all done automatically.
